Medidas de tendencia central: Media, Mediana, Moda

Ahora nos ocuparemos exclusivamente de las variables cuantitativas, puesto que con los atributos no se pueden realizar operaciones aritméticas. Como hemos estudiado, las variables estadísticas cuantitativas se dividen o clasifican en discretas o continuas, por lo que necesitaremos precisar cómo se calculan dichas medidas en cada caso.

Las medidas estadísticas pretenden "resumir" la información de la "muestra" para poder tener así un mejor conocimiento de la población.

Las medidas de tendencia central corresponden a valores que generalmente se ubican en la parte central de un conjunto de datos. (Ellas permiten analizar los datos en torno a un valor central). Entre éstas están la media aritmética, la moda y la mediana.

a) Media aritmética _
( X )

Es aquella medida que se obtiene al dividir la suma de todos los valores de una variable por la frecuencia total. En palabras más simples, corresponde a la suma de un conjunto de datos dividida por el número total de dichos datos.

X = suma de todos los valores = x1 + x2 + x3 + x4 + ......
número total de datos n

Ejemplo 1:

En matemáticas, un alumno tiene las siguientes notas: 4, 7, 7, 2, 5, 3

n = 6 (número total de datos )

X = 4 + 7 + 7 + 2 + 5 + 3 = 28 = 4,8
6 6

La media aritmética de las notas de esa asignatura es 4,8. Este número representa el promedio.

Ejemplo 2:

Cuando se tienen muchos datos es más conveniente agruparlos en una tabla de frecuencias y luego calcular la media aritmética. El siguiente cuadro lo ilustra.

Largo (en m)
Frecuencia absoluta
Largo por Frecuencia absoluta

3
10
5 . 10 = 50

6
15
6 . 15 = 90

7
20
7 . 20 = 140

8
12
8 . 12 = 96

9
6
9 . 6 = 54

Frecuencia total = 63
430


X = 430 = 6,825
63

Se debe recordar que la frecuencia absoluta indica cuántas veces se repite cada valor, por lo tanto, la tabla es una manera más corta de anotar los datos (si la frecuencia absoluta es 10, significa que el valor a que corresponde se repite 10 veces).

b) Moda (Mo)

Es la medida que indica cual dato tiene la mayor frecuencia en un conjunto de datos, o sea, cual se repite más.

Ejemplo 1:

Determinar la moda en el siguiente conjunto de datos que corresponden a las edades de niñas de un Jardín Infantil.

5, 7, 3, 3, 7, 8, 3, 5, 9, 5, 3, 4, 3

La edad que más se repite es 3, por lo tanto, la Moda es 3 (Mo = 3)

Ejemplo 2:

20, 12, 14, 23, 78, 56, 96

En este conjunto de datos no existe ningún valor que se repita, por lo tanto, este conjunto de valores no tiene moda.

c) Mediana (Med)

Es el valor central de un conjunto de valores ordenados en forma creciente o decreciente. Dicho en otras palabras, la Mediana corresponde al valor que deja igual número de valores antes y después de él en un conjunto de datos agrupados.

Según el número de valores que se tengan se pueden presentar dos casos:

- Si el número de valores es impar, la Mediana corresponderá al valor central de dicho conjunto de datos.

- Si el número de valores es par, la Mediana corresponderá al promedio de los dos valores centrales (los valores centrales se suman y se dividen por 2).

Ejemplo 1:

Se tienen los siguientes datos: 5, 4, 8, 10, 9, 1, 2

Al ordenarlos en forma creciente, es decir de menor a mayor, se tiene:

1, 2, 4, 5 , 8, 9, 10

El 5 corresponde a la Med, porque es el valor central en este conjunto de datos impares.

Ejemplo 2:

El siguiente conjunto de datos está ordenado en forma decreciente, de mayor a menor, y corresponde a un conjunto de valores pares, por lo tanto, la Med será el promedio de los valores centrales.

21, 19, 18, 15, 13, 11 ,10, 9, 5, 3

Med = 13 + 11 = 24 = 12
2 2

Ejemplo 3:



En el gráfico de barras (que tiene un número par de columnas) los valores centrales son 72 y 77, por lo tanto, la

Med = 72 + 77 = Med = 149 = 74,5

2 2

Teoria de conteo

Técnicas de Conteo

Si el número de posibles resultados de un experimento es pequeño, es relativamente fácil listar y contar todos los posibles resultados. Al tirar un dado, por ejemplo, hay seis posibles resultados.

Si, sin embargo, hay un gran número de posibles resultados tales como el número de niños y niñas por familias con cinco hijos, sería tedioso listar y contar todas las posibilidades.

Las posibilidades serían, 5 niños, 4 niños y 1 niña,


3 niños y 2 niñas, 2 niños y 3 niñas, etc. Para facilitar el conteo examinaremos tres técnicas: La técnica de la multiplicación, la técnica de la permutación, y la técnica de la combinación.

La Técnica de la Multiplicación

La técnica de la multiplicación: Si hay m formas de hacer una cosa y hay n formas de hacer otra cosa, hay m x n formas da hacer ambas cosas

En términos de fórmula

Número total de arreglos = m x n

Esto puede ser extendido a más de dos eventos. Para tres eventos, m, n, y o:

Número total de arreglos = m x n x o

Ejemplo:

Un vendedor de autos quiere presentar a sus clientes todas las diferentes opciones con que cuenta: auto convertible, auto de 2 puertas y auto de 4 puertas, cualquiera de ellos con rines deportivos o estándar. ¿Cuántos diferentes arreglos de autos y rines puede ofrecer el vendedor?

Para solucionar el problema podemos emplear la técnica de la multiplicación, (donde m es número de modelos y n es el número de tipos de rin).

Número total de arreglos = 3 x 2

No fue difícil de listar y contar todos los posibles arreglos de modelos de autos y rines en este ejemplo. Suponga, sin embargo, que el vendedor tiene para ofrecer ocho modelos de auto y seis tipos de rines. Sería tedioso hacer un dibujo con todas las posibilidades. Aplicando la técnica de la multiplicación fácilmente realizamos el cálculo:

Número total de arreglos = m x n = 8 x 6 = 48

Area bajo la curva

AREAS BAJO LA CURVA NORMAL Conceptos preliminares: La Distribución Normal: Es una distribución cuyas variables aleatorias pueden tomar un número infinito de
posibles valores, o cuyas diferencias entre si pueden ser infinitesimales; por lo tanto es
una distribución continua, ya que sus variables pueden medirse con el grado de

precisión que se desee.
Algunos ejemplos de variables continuas son las medidas de:
. Tiempo (años, meses, días, horas, minutos, segundos, etc.)
. Distancia (Km, metros, centímetros, milímetros, etc.)
. Estatura
. Peso
. Coeficiente intelectual CI (IQ)

Importancia de la Distribución Normal: • Existen numerosas variables que parecen seguir una forma similar a la
distribución normal (pesos, alturas, coeficientes intelectuales, calificaciones en
exámenes, etc.)

• La distribución muestral de muchos estadígrafos muestrales como la media
tienen una distribución aproximadamente normal e independiente de la
configuración de la población, si los datos son suficientemente numerosos.

• Es una excelente aproximación a otras distribuciones muestrales como la de Poisson y Binomial, por ejemplo. • La Función Normal: Es una curva lisa, de forma acampanada y unimodal como se presenta en la figura 1.1

Distribucion binominal

La distribuci´on binomial o de Bernoulli

La distribuci´on binomial est´a asociada a experimentos del siguiente tipo:

- Realizamos n veces cierto experimento en el que consideramos s´olo la posibilidad de ´exito o

fracaso.

- La obtenci´on de ´exito o fracaso en cada ocasi´on es independiente de la obtenci´on de ´exito o

fracaso en las dem´as ocasiones.

- La probabilidad de obtener ´exito o fracaso siempre es la misma en cada ocasi´on.

Ve´amoslo con un

ejemplo

Tiramos un dado 7 veces y contamos el n´umero de cincos que obtenemos. .Cu´al es la probabilidad

de obtener tres cincos?.

Este es un t´ıpico ejemplo de distribuci´on binomial, pues estamos repitiendo 7 veces el experimento

de lanzar un dado. .Cu´al es nuestro ´exito?.

Evidentemente, sacar un 5, que es en lo que nos fijamos.

El fracaso, por tanto, ser´a no sacar 5, sino sacar cualquier otro n´umero.

Por tanto, ´Exito = E = “sacar un 5” =

1

6

Fracaso = F = “no sacar un 5” =

5

6

Para calcular la probabilidad que nos piden, fij´emonos en que nos dicen que sacamos 3 cincos y

por lo tanto tenemos 3 ´exitos y 4 fracasos, .de cu´antas maneras pueden darse estas posibilidades?.

Podr´ıamos sacar 3 cincos en las 3 primeras tiradas y luego 4 tiradas sin sacar cinco, es decir: EEEFFFF

Pero tambi´en podr´ıamos sacar EFEFFFE, es decir que en realidad estamos calculando de cu´antas

38

⇒ p(E) =⇒ p(F) =

CAP´ITULO 3. DISTRIBUCI´ ON BINOMIAL Y DISTRIBUCI´ ON NORMAL

maneras se pueden ordenar 4 fracasos y 3 ´exitos. Recordando las t´ecnicas combinatorias, este problema

se reduce a calcular las permutaciones con elementos repetidos:

39

P

7

7!

3!

=

7

3

= 35formas

Y por tanto, como

1

6

y tengo 3 ´exitos y

5

6

y tengo 4 fracasos:

3,4=・ 4!・ 6 ・ 5・ 2 ・ 1p(E) =p(F) =

p

(tener 3 ´exitos y 4 fracasos) = 35 ・

1

6

・

1

6

・

1

6

・

5

6

・

5

6

・

5

6

・

5

6

= 0

Formalizando lo obtenido, en una variable binomial con 7 repeticiones y con probabilidad de ´exito

1

6

,

la probabilidad de obtener 3 ´exitos es 0’0781, y lo expresar´ımos:

Bin

0781

7;

1

6

,

Como repetir este proceso ser´ıa bastante penoso en la mayor´ıa de los casos, lo mejor es recurrir a la

siguiente f´ormula que expresa la probabilidad de obtener cierto n´umero de ´exitos en una distribuci´on

binomial:

entonces p(X = 3) = 0 0781

Definici´on de distribuci´on binomial:

Si realizamos n veces un experimento en el que podemos obtener ´exito, E, con probabilidad p y

fracaso, F, con probabilidad q (

par´ametros n y p, y lo representaremos por Bin(n;p). En este caso la probabilidad de obtener k ´exitos

viene dada por:

q = 1 − p), diremos que estamos ante una distribuci´on binomial de

p

(X = k) =

n

k

・

pk ・ q(n−k)

Nota:

Observar que las probabilidades de ´exito y fracaso son complementarias, es decir, q = 1-p y p =

1-q, por lo que basta saber una de ellas para calcular la otra.

Ejemplo:

Antes ten´ıamos Bin

7;

1

6

, y quer´ıamos calcular p(X=3) (obtener 3 ´exitos). Aplicando la f´ormula:

p

(X = 3) =

7

3

・

1

6

3

・

5

6

4

= 0

0781

Ejemplo:

Supongamos que la probabilidad de que una pareja tenga un hijo o una hija es igual. Calcular la

probabilidad de que una familia con 6 descendientes tenga 2 hijos.

En este caso ´Exito = E = “tener hijo” y p(E) = 0’5.

Fracaso = F = “tener hija” y p(F) = 0’5.

Estamos por tanto ante una binomial Bin(6;0’5) y nos piden p(X=2).

Si aplicamos la f´ormula es:

p

(X = 2) =

6

2

・

(0 5)2 ・ (0 5)4 = 0 2344

Nota:

La elecci´on de ´exito o fracaso es subjetiva y queda a elecci´on de la persona que resuelve el problema,

pero teniendo cuidado de plantear correctamente lo que se pide. En el caso concreto del ejemplo

anterior, si:

´Exito =

“

tener hija”, como nos piden la probabilidad de que una familia con 6

hijos tenga 2

hijos,

si el ´exito es tener hija hemos de plantearnos cu´al es la probabilidad de tener 4 ´exitos (4 hijas), es

Diagrama de arbol

I. DIAGRAMA DE ARBOL.

Un diagrama de árbol es una representación gráfica de un experimento que consta de r pasos, donde cada uno de los pasos tiene un número finito de maneras de ser llevado a cabo.

Ejemplos:

1.Un médico general clasifica a sus pacientes de acuerdo a: su sexo (masculino o femenino), tipo de sangre (A, B, AB u O) y en cuanto a la presión sanguínea (Normal, Alta o Baja). Mediante un diagrama de árbol diga en cuantas clasificaciones pueden

estar los pacientes de este médico?                                  

                                                                                  N

Solución:                                                                   A

                                                           A                     B

                                                                                  N

                                                           B                     A

                                                                                  B

                                   M                    AB                  N

                                                                                  A                                

                                                           O                     B

                                                          

                                                                                   

                                                           A

                                                                                  N

                                   F                     B                     A

                                                                                  B

                                                           AB

                                                                                  B

                                                           O                     A

                                                                           

                                                                            B

                                                                           

Si contamos todas las ramas terminales, nos damos cuenta que el número de clasificaciones son  2 x 4 x 3 = 24 mismas que podemos enumerar;

MAN, MAA, MAB, MBN, MBA, MBB, etc, etc.

1)      Dos equipos denominados A y B se disputan la final de un partido de baloncesto, aquel equipo que gane dos juegos seguidos o complete un total de tres juegos ganados será el que gane el torneo. Mediante un  diagrama de árbol diga de cuantas maneras puede ser ganado este torneo,

Solución:

A = gana el equipo A

B = gana el equipo B

                                         A

                                                                                        A

                  A                                            A

                                         B                                                                    A                    

                                                                                        B

                                                                 B                                            B

                                                                 A

                                         A                                                                    A

                                                                                        A

                  B                                            B                                            B

                                         B

                                                                                        B

En este diagrama se muestran que hay solo diez maneras de que se gane el torneo, que se obtienen contando las ramas terminales de este diagrama de árbol, las que es posible enumerar;

AA, ABB, ABAA, ABABA, ABABB, etc, etc.

2)      Un hombre tiene tiempo de jugar ruleta cinco veces como máximo, él empieza a jugar con un dólar, apuesta cada vez un dólar y puede ganar o perder en cada juego un dólar, él se va a retirar de jugar si pierde todo su dinero, si gana tres dólares (esto es si completa un total de cuatro dólares) o si completa los cinco juegos, mediante un diagrama de árbol, diga cuántas maneras hay de que se efectué el juego de este hombre.

Solución:

                                                                           

                                                                 $4                                           G $4

                                               G                     $3                   

                                         $3                                           G

                                               G                                                                    P $2                           

                                                                       P                                             G$3

                                                                       $2                    P

                                                                                              $1                    P $0

                                                                                              $3                    G $4

                                 $2                                                          G

            $1                    G                                $2

G                                            P $2

                                                                                                                      G $2

                                               P                                             P

                                               $1                    P                     $1                   

                                   P                                 $0                                           P $0

$0

Si contamos las ramas terminales nos daremos cuenta que hay 11 maneras de que este hombre lleve a cabo sus apuestas, en este diagrama se han representado los cinco juegos  o apuestas que este hombre tiene tiempo de jugar.

combinaciones

Combinaciones

También hay dos tipos de combinaciones (recuerda que ahora el orden no importa):

1. Se puede repetir: como monedas en tu bolsillo (5,5,5,10,10)
2. Sin repetición: como números de lotería (2,14,15,27,30,33)

1. Combinaciones con repetición

En realidad son las más difíciles de explicar, así que las dejamos para luego.

2. Combinaciones sin repetición

Así funciona la lotería. Los números se eligen de uno en uno, y si tienes los números de la suerte (da igual el orden) ¡entonces has ganado!

La manera más fácil de explicarlo es:

• imaginemos que el orden sí importa (permutaciones),
• después lo cambiamos para que el orden no importe.

Volviendo a las bolas de billar, digamos que queremos saber qué 3 bolas se eligieron, no el orden.

Ya sabemos que 3 de 16 dan 3360 permutaciones.

Pero muchas de ellas son iguales para nosotros, porque no nos importa el orden.

Por ejemplo, digamos que se tomaron las bolas 1, 2 y 3. Las posibilidades son:

El orden importa	El orden no importa
1 2 3 1 3 2 2 1 3 2 3 1 3 1 2 3 2 1	1 2 3

Así que las permutaciones son 6 veces más posibilidades.

De hecho hay una manera fácil de saber de cuántas maneras "1 2 3" se pueden ordenar, y ya la sabemos. La respuesta es:

3! = 3 × 2 × 1 = 6

(Otro ejemplo: 4 cosas se pueden ordenar de 4! = 4 × 3 × 2 × 1 = 24 maneras distintas, ¡prueba tú mismo!)

Así que sólo tenemos que ajustar nuestra fórmula de permutaciones para reducir por las maneras de ordenar los objetos elegidos (porque no nos interesa ordenarlos):

Esta fórmula es tan importante que normalmente se la escribe con grandes paréntesis, así:

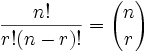donde n es el número de cosas que puedes elegir, y eliges r de ellas (No se puede repetir, el orden no importa)

Y se la llama "coeficiente binomial".

Notación

Además de los "grandes paréntesis", la gente también usa estas notaciones:

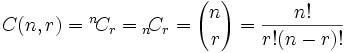
Ejemplo

Entonces, nuestro ejemplo de bolas de billar (ahora sin orden) es:

16!	=	16!	=	20,922,789,888,000	= 560
3!(16-3)!		3!×13!		6×6,227,020,800

O lo puedes hacer así:

16×15×14	=	3360	= 560
3×2×1		6

Así que recuerda, haz las permutaciones, después reduce entre "r!"

... o mejor todavía...

¡Recuerda la fórmula!

Es interesante darse cuenta de que la fórmula es bonita y simétrica:

Con otras palabras, elegir 3 bolas de 16 da las mismas combinaciones que elegir 13 bolas de 16.

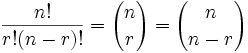
16!	=	16!	=	16!	= 560
3!(16-3)!		13!(16-13)!		3!×13!

Triángulo de Pascal

Puedes usar el triángulo de Pascal para calcular valores. Baja a la fila "n" (la de arriba es n=0), y ve a la derecha "r" posiciones, ese valor es la respuesta. Aquí tienes un trozo de la fila 16:

1    14    91    364  ...
1    15    105   455   1365  ...
1    16   120   560   1820  4368  ...

1. Combinaciones con repetición

OK, ahora vamos con este...

Digamos que tenemos cinco sabores de helado: banana, chocolate, limón, fresa y vainilla. Puedes tomar 3 paladas. ¿Cuántas variaciones hay? Vamos a usar letras para los sabores: {b, c, l, f, v}. Algunos ejemplos son {c, c, c} (3 de chocolate) {b, l, v} (uno de banana, uno de limón y uno de vainilla) {b, v, v} (uno de banana, dos de vainilla)

(Y para dejarlo claro: hay n=5 cosas para elegir, y eliges r=3 de ellas.
El orden no importa, ¡y sí puedes repetir!)

Bien, no puedo decirte directamente cómo se calcula, pero te voy a enseñar una técnica especial para que lo averigües tú mismo.

	Imagina que el helado está en contenedores, podrías decir "sáltate el primero, después 3 paladas, después sáltate los 3 contenedores siguientes" ¡y acabarás con 3 paladas de chocolate!
	Entonces es como si ordenaras a un robot que te trajera helado, pero no cambia nada, tendrás lo que quieres.

Ahora puedes escribirlo como  (la flecha es saltar, el círculo es tomar)

Entonces los tres ejemplos de arriba se pueden escribir así:

{c, c, c} (3 de chocolate):
{b, l, v} (uno de banana, uno de limón y uno de vainilla):
{b, v, v} (uno de banana, dos de vainilla):

OK, entonces ya no nos tenemos que preocupar por diferentes sabores, ahora tenemos un problema más simple para resolver: "de cuántas maneras puedes ordenar flechas y círculos"

Fíjate en que siempre hay 3 círculos (3 paladas de helado) y 4 flechas (tenemos que movernos 4 veces para ir del contenedor 1º al 5º).

Así que (en general) hay r + (n-1) posiciones, y queremos que r de ellas tengan círculos.

Esto es como decir "tenemos r + (n-1) bolas de billar y queremos elegir r de ellas". Es decir, es como el problema de elegir bolas de billar, pero con números un poco distintos. Lo podrías escribir así:

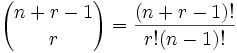donde n es el número de cosas que puedes elegir, y eliges r de ellas (Se puede repetir, el orden no importa)

Es interesante pensar que podríamos habernos fijado en flechas en vez de círculos, y entonces habríamos dicho "tenemos r + (n-1) posiciones y queremos que (n-1) tengan flechas", y la respuesta sería la misma...

¿Qué pasa con nuestro ejemplo, cuál es la respuesta?

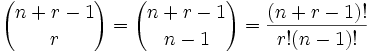
(5+3-1)!	=	7!	=	5040	= 35
3!(5-1)!		3!×4!		6×24